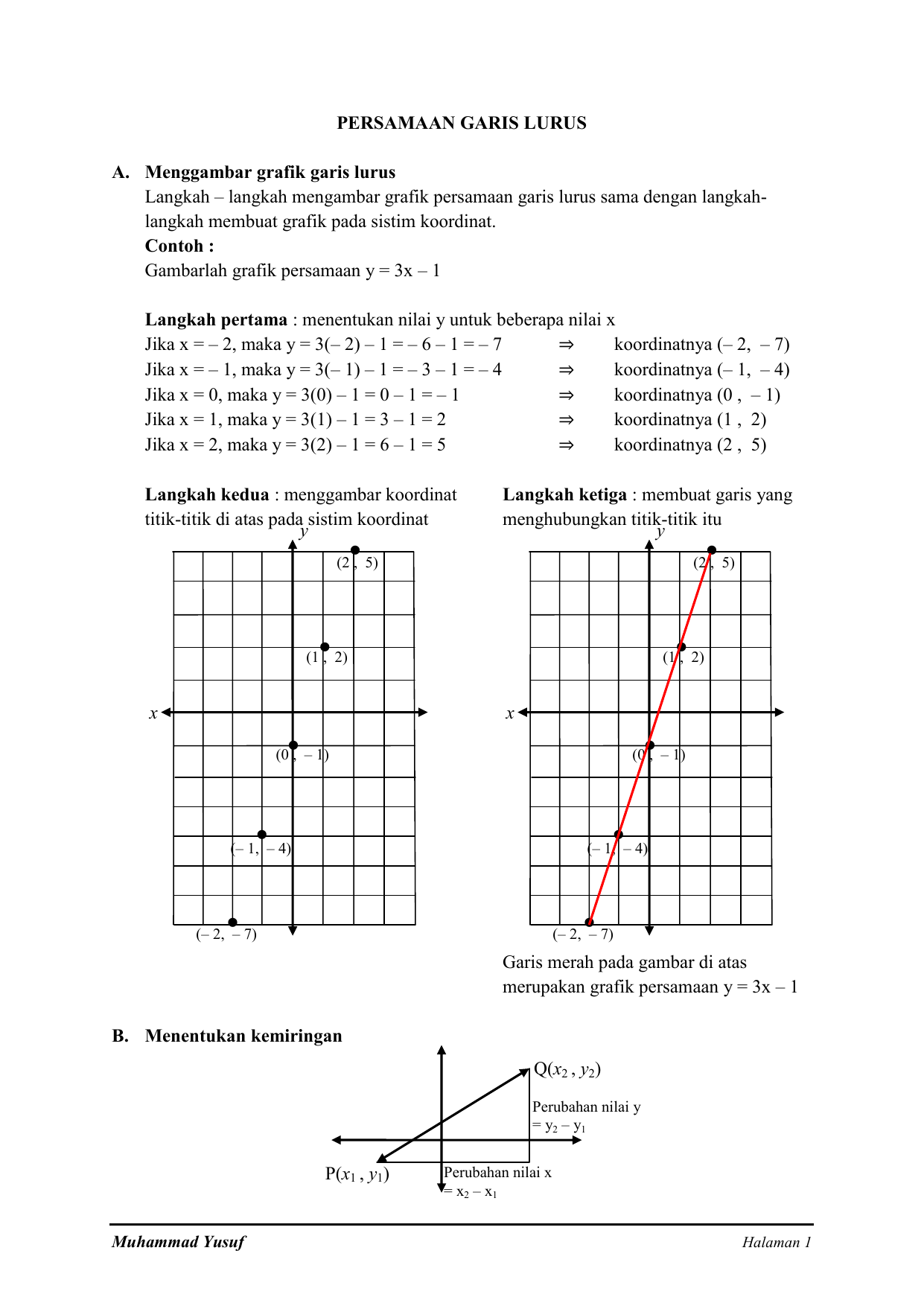
Bentuk Persamaan Garis Lurus Dengan Kemiringan M Dan Melalui Titik X1 Y1

Mencari informasi terkait Bentuk Persamaan Garis Lurus Dengan Kemiringan M Dan Melalui Titik X1 Y1.

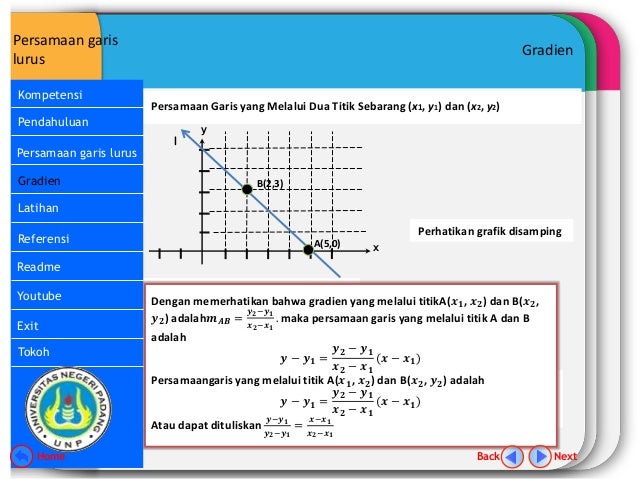
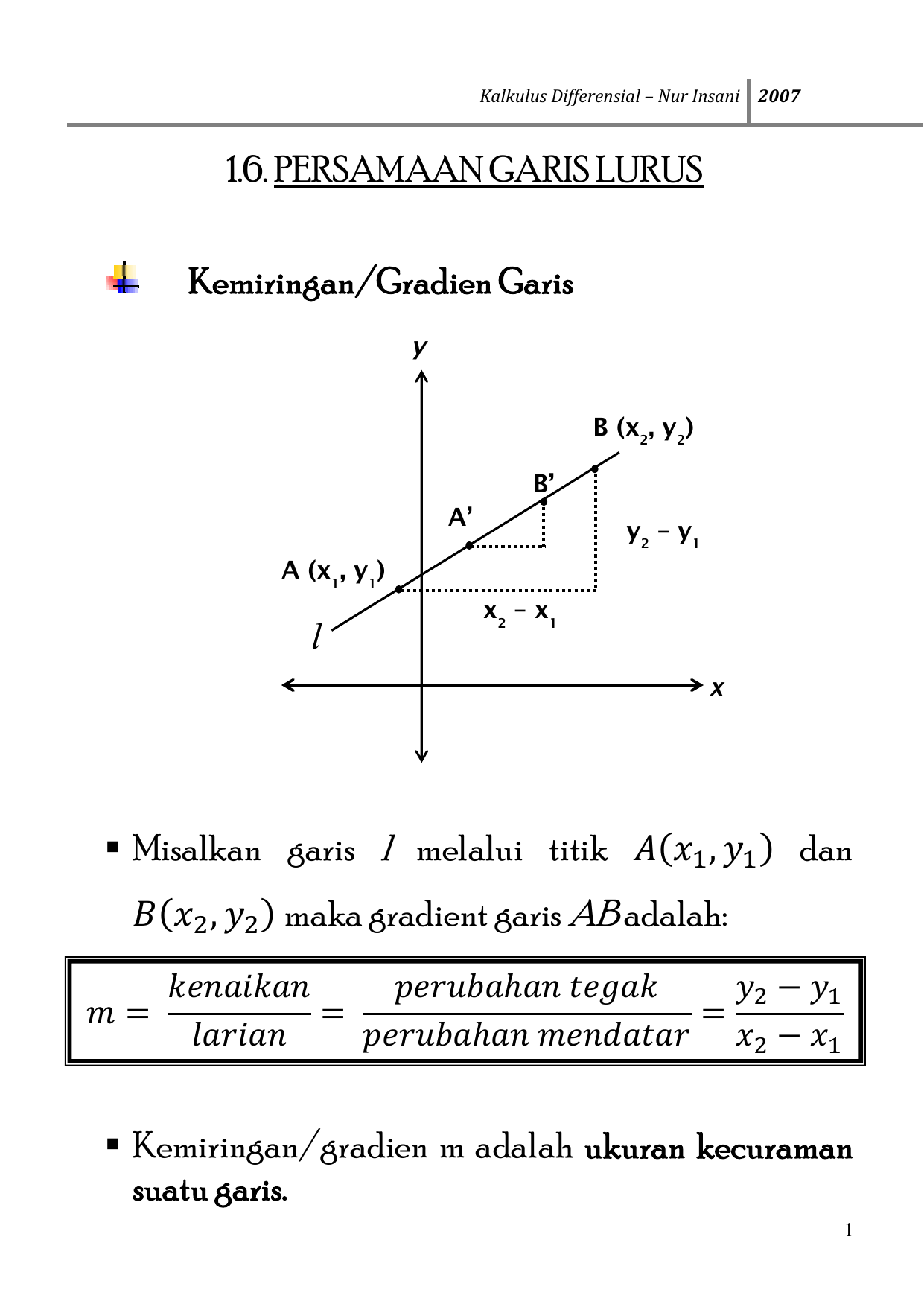
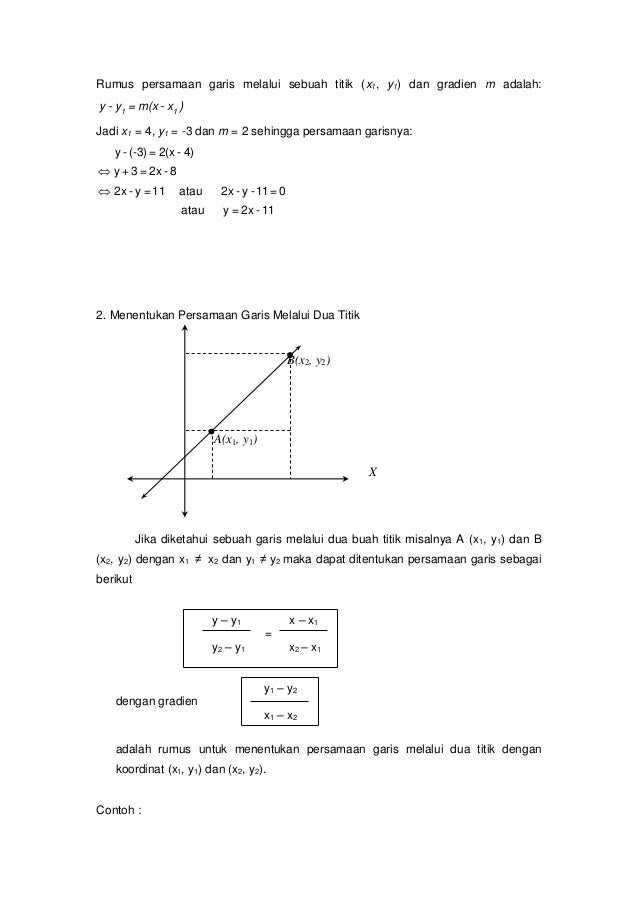
Y y1 m x x1. Dengan menggunakan rumus persamaan garis dengan gradient m dan melalui sebuah titik x1 y1 yaitu y y1 m x x1 dapat diperoleh rumus berikut.

Matematika Buku Guru2 Pages 151 200 Text Version Fliphtml5

Media

Sistem Koordinat Ppt Download

Doc Tugas Buku Gradien Garis Dan Persamaan Garis Yovita Maya

16 Persamaan Garis Lurus Kemiringangradien Garis

Matematika Kelas 8 Cara Mencari Kemiringan Gradien Pada Garis Lurus

21 Garis Lurus Melalui Titik Asal 00 22 Bentuk

Kalkulator Online Persamaan Garis Lurus Antara Dua Titik

Persamaan Garis Lurusdocx

Persamaan Garis Lurus Yang Melewati Dua Titik De Eka

Materi Labarasi

Menyelesaikan sistem persamaan linear dua variabel dengan eliminasi c.

Bentuk persamaan garis lurus dengan kemiringan m dan melalui titik x1 y1. Sifat sifat persamaan garis lurus. Bab 5 sistem persamaan linear dua variabel a. 2tentukan persamaan garis yang tegak lurus dengan garis y4 x dan melalui titik 51.

Pada episode kali ini kak wahyu membahas materi contoh soal persamaan garis lurus yang bergradien m dan melalui titik x1 y1 untuk kelas 8viii. Dengan menggunakan rumus persamaan garis dengan gradient m dan melalui sebuah titik x1 y1 yaitu y y1 m x x1 dapat diperoleh rumus berikut. Misal titik 1 adalah x1 y1 0 6 dan titik 2 x2 y2 3 0 masukkan rumus yang sama dengan angka yang telah kita balik tadi ternyata hasilnya adalah sama jadi ambil saja sembarang tak perlu pusing dengan mana titik satu mana titik 2.

Y y1 m x x1. Menentukan kemiringan persamaan garis lurus c. 1tentukan persamaan garis yang tegak lurus dengan garis 2x 4y5 dan melalui titik 10.

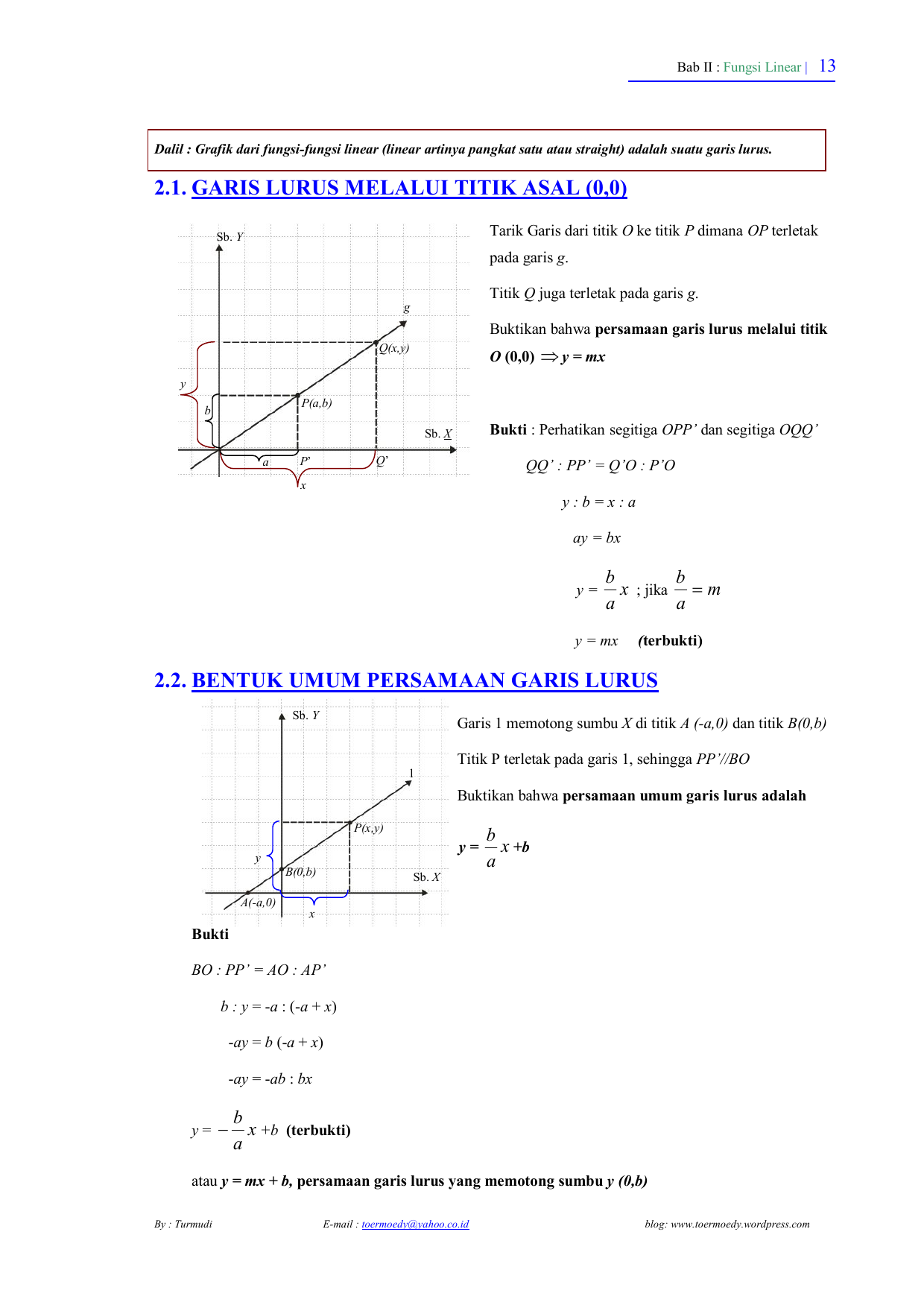
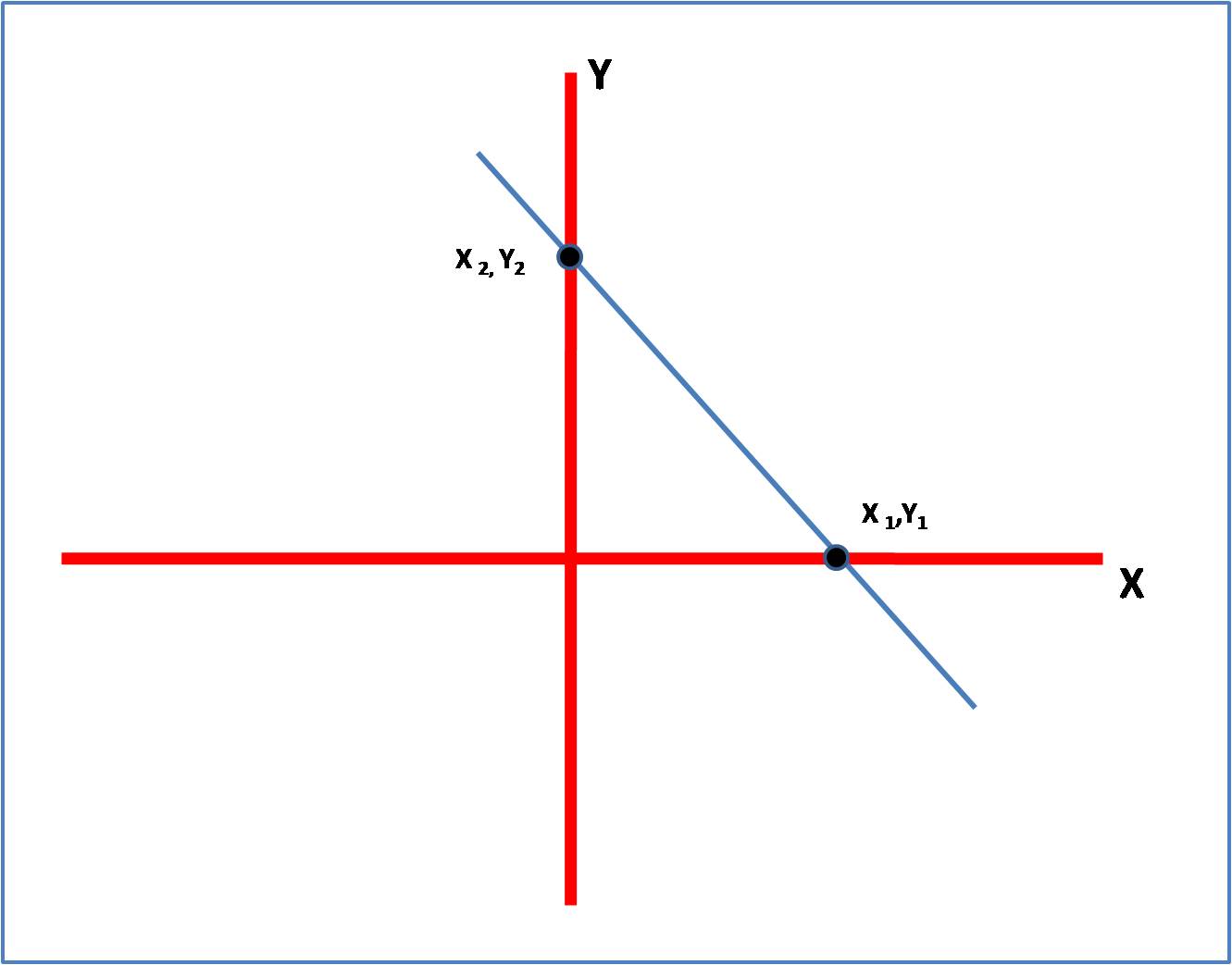
Sebuah garis lurus dapat diperoleh dengan cara menguhubungkan dua titik sembarang misal titik p x1 y1 dan q x2 y2 gradien garis pq m delta y delta x y2 y1x2 x1. Ringkasan teori a gradien garis lurus adalah gradien garis lurus atau koefisien garis adalah ukuran kemiringan suatu garis terhadap sumbu x positif. Dengan menggunakan rumus persamaan garis dengan gradient m dan melalui sebuah titik x1 y1 yaitu y y1 m x x1 dapat diperoleh rumus berikut.

Menyelesaikan sistem persamaan linear dua variabel dengan. Bentuk persamaan garis lurus dengan kemiringan m dan melalui titik x1 y1 d. Memahami konsep persamaan linear dua variabel b.

Inti dari persamaan garis lurus adalah memahami apa itu gradien dan memahami antara titik yang dilalui baik titik pusat koordinat titik koordinat y ataupun titik koordinat x. Y y1 m x x1. Atau jika dilambangkan yaitu titik pusat koordint 0 0 titik koordinat x1 y1 dan x2 y 2.

bentuk persamaan garis lurus dengan kemiringan m dan melalui titik x1 y1 Bentuk ialah satu titik temu antara ruang dan massa.Bentuk juga merupakan penjabaran geometris dari bagian semesta bidang yang di tempati oleh objek tersebut, yaitu ditentukan oleh batas-batas terluarnya namun tidak tergantung pada lokasi (koordinat) dan orientasi (rotasi)-nya terhadap bidang semesta yang di tempati.

Itulah informasi tentang bentuk persamaan garis lurus dengan kemiringan m dan melalui titik x1 y1 yang dapat admin kumpulkan. Admin dari blog Berbagi Bentuk 2019 juga mengumpulkan gambar-gambar lainnya terkait bentuk persamaan garis lurus dengan kemiringan m dan melalui titik x1 y1 dibawah ini.

Doc Persamaan Garis Lurus Lidya Christiani Academiaedu

Persamaan Garis Program Studi Pendidikan Matematika Oleh Kelompok 4

4tentukan Persamaan Garis Lurus Jika Diketahui Informasi Berikut

Bab Xi Persamaan Garis Lurus Pdf Document

Persamaan Garis Lurusdocx

Kelompok Ii Persamaan Garis Lurus

Matematika Soal Pembahasan Gradien Dan Persamaan Garis Lurus

Bab Xi Persamaan Garis Lurus Pdf Document

Kelas 08 Smp Matematika S1 Siswa 2017 By Pe Thea Issuu

Persamaan Garis Lurus

Garis Lurus

Doc Bab Iii Persamaan Garis Lurus Mts Al Mawaddah Academiaedu

Itulah yang admin bisa dapat mengenai bentuk persamaan garis lurus dengan kemiringan m dan melalui titik x1 y1. Terima kasih telah berkunjung ke blog Berbagi Bentuk 2019.